金澤は確率過程の統計物理学に関わる研究者であり,広い意味での統計物理学の様々なテーマに興味があります.金澤が今興味がある内容を記載します注1.
全テーマに共通すること
金澤の研究テーマは多岐にわたりますが,すべてに共通することは確率過程論を駆使することです.金澤は一言で言えば『物理周辺の確率過程の専門家』だと思います(といっても数学者ではないので純粋数学としての確率過程についてはあまりわかりませんが).なので,金澤研に入った場合,全員が必ず確率過程を自由自在に扱えるようになって貰おうと思っています.
金澤が興味を持つテーマ
現在,金澤が最も興味を持っているのは,
- 確率過程の基礎研究(特に非マルコフ過程)
- 金融市場の経済物理学
- 非平衡揺らぎの統計物理学
です.現時点で最も研究成果(具体的には論文)が出そうだと見込んでいて投資したいのは『経済物理学』の研究テーマです.また,非マルコフ過程基礎論も今までの投資成果が出てきていますので,理論家としては今が収穫のフェーズだと思っています.また,確率過程の基礎研究・非平衡統計物理の研究はライフワークだと思っています.以下,順に説明します注2.
注1:[よくある質問] 金澤の興味と離れたテーマは選べますか?
必ずしもこの内容と同じテーマを選ぶ必要はないです.特に博士課程進学を考えている理論志望の学生は,金澤の興味から離れた研究テーマを選択して頂いてもよいです(全く離れてしまうと適切に指導ができませんが).
注2:雑誌名の略称
- PRL = Physical Review Letters
- PRE = Physical Review E
- PRR = Physical Review Research
- JSP = Journal of Statistical Physics
- 確率過程
- 経済物理学
- 揺らぎの統計物理学
確率過程の基礎研究
金澤は「風変りな確率過程」の理論研究全般に興味があります.たとえば異常拡散と関係する確率過程の数理(例えばレヴィ・フライト,Nature 2020)を研究しています.また非マルコフ過程の代表例として,ホークス過程と呼ばれる臨界現象の確率モデルの研究もしています (PRL 2020).非マルコフ過程は数学的に解くことが難しいクラスに属しますが,金澤は非マルコフ過程を扱う新しい数学技法の開発に,今理論的には最も興味を持っています.
非マルコフ過程
確率過程論では,現在の情報によって1ステップ未来の動きが決まるモデルをマルコフ過程と呼びます.一方,非マルコフ過程とはそうではなく,過去全ての情報が関わるクラスです.非マルコフ過程は非常に数学的に難しいクラスであり,殆ど解析手法が確立していません.
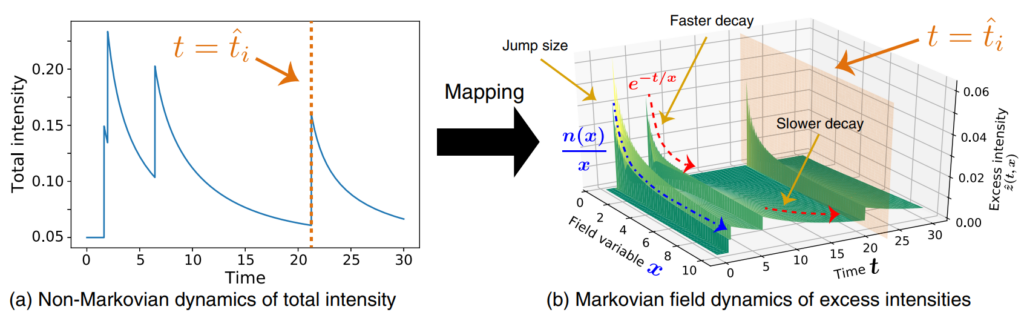
金澤は非マルコフ過程を扱う新しい解析方法を開発することに挑戦しています.具体的な例として,ホークス過程(や一般化ランジュバン方程式)を扱ったのがPRL 2020, PRL 2021になります.これらの論文では,非マルコフ過程に対して適切な補助場変数を導入すること(マルコフ埋め込みと呼ばれる手法)で,マルコフ場の理論に変形するアプローチを提案しています.マルコフ場の確率過程に対して,場のマスター方程式を導出することで,非マルコフ過程を解析的に扱うことに成功しています.
金澤はこのアプローチはホークス過程のみならずより広い非マルコフ過程に使える汎用手法だと考えており,現在研究しています.具体的には,任意の非マルコフ過程に対してマスター方程式を導出し,場の理論として包括的に取り扱うスキームの開発に興味があります.
経済物理学(金融)

金澤は広い意味で,確率過程周辺の統計物理学の学際研究に興味があります.現時点で最も興味があり,なおかつ,最も見込みがあると思って投資したいのは金融市場の経済物理学です.また,学生が論文を書く上でも,最もテーマ選択で困らないトピックだと思っています.
我々は株式市場・外為市場のミクロデータを分析し,トレーダーの市場での売買戦略を分析しています.そして,トレーダー個々人の注文行動の動力学を確率過程を用いてエージェントベースモデル(ABM)としてモデル化し,統計物理学にルーツを持つ理論手法を用いてミクロからマクロを解明する研究を行っています.
ミクロデータ=個々人レベルのオークションデータ
まずはミクロデータ解析についてです.ここでいうミクロデータというのは,金融市場(株式・外為)ともに『個々人レベルのオークションデータ』を指しています.機関投資家が活動する多くの金融市場では,連続時間の両側オークションを行いながら売買を行います.具体的には,将来的に通貨・株式の売買を行ってもよいと考えるトレーダーは希望する買値(売値)を指定した上で注文を出します(指値注文).現代では取引の高度な電子化が進んでおり,こういったトレーダーの売買行動が完全に電子データ化されています.
下にオークションの注文分布(オーダーブックと言います)の動画を示します.青のブロックが買い注文で,赤のブロックが売り注文です(例えば172円に青ブロックがvolume=100で置いてあれば,172円で100単位の株式購入の意思を示した=入札したことになります).買い注文と売り注文が押し合いへし合いして,価格が形成されていきます.テトリスに近いようなイメージですが,我々はこういった注文の「ブロック」の動力学を,個々人の意思決定のレベルのデータを元に研究しています.
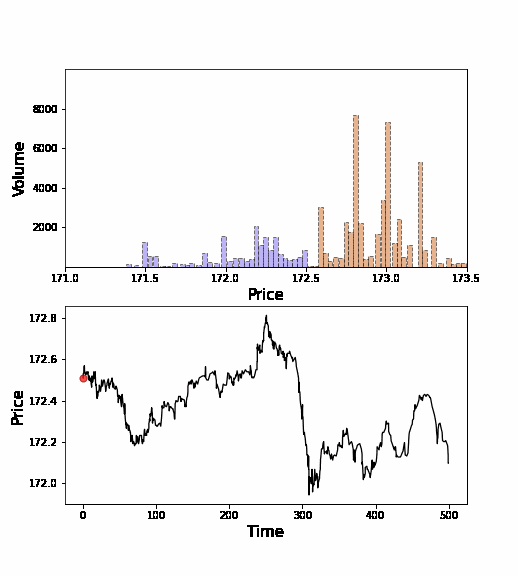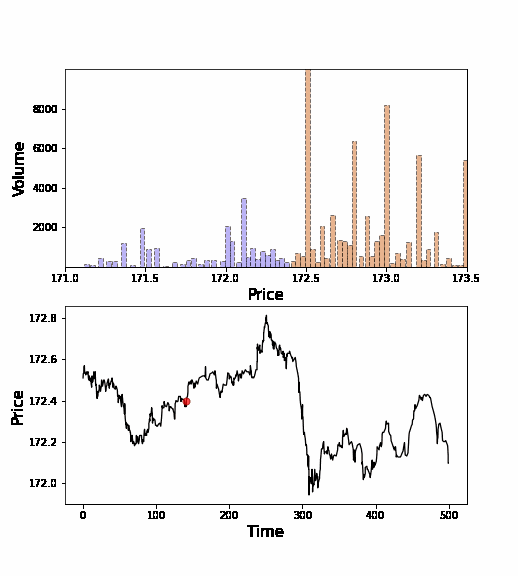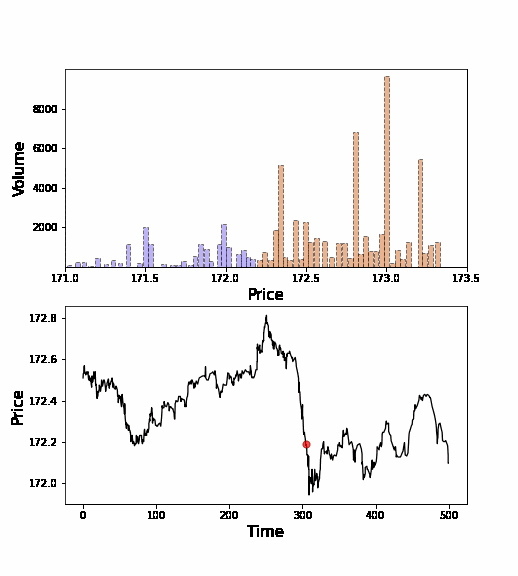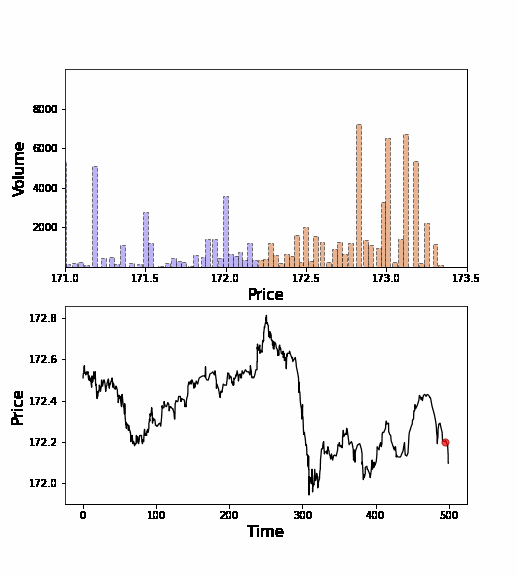
ミクロデータには個々のトレーダーの取引戦略が反映されていることが期待されます.そこで,どのような取引戦略が採用されているかを,個々人の注文行動の統計分析を通じて理解することを行っています.例えば,「過去の取引価格時系列から見えるトレンド(モメンタム)に対して,個々人はどう応答するか?」という問を,トレンドフォロー戦略の観点から論文(PRL 2018, PRE 2018, PloS ONE 2018)で調べました.このように,注文行動を分析することで,データ解析から帰納的にミクロ数理モデルを構築することを行っています.
金融市場の『統計物理学』
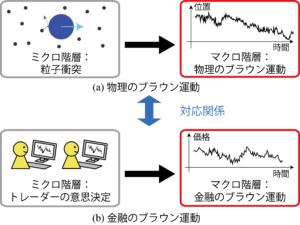
上記の統計解析には特に『物理っぽさ』はありません.これは経済現象をあつかっているので当たり前だと思います(色々な研究のアプローチがありますが,あまり金澤は現象的なアナロジーは重要視していません).一方で,理論モデルを作っていくと,物理学で発達してきた考え方が部分部分として役立つことがあります.実際,金澤は統計物理学の計算理論を用いて,金融市場のモデルを解析することを行っています.
まず,データ解析を通じて金融市場におけるミクロなダイナミクスを(観測可能な行動レベルで)推定することを行います.この結果をABMとして数理モデル化します.トレーダーの行動は決定論的であることは期待できないため,ABMは確率過程としてモデル化することになります.すなわち,データ解析を反映させるための数理モデルとして,多体系の確率過程(確率微分方程式)を採用します.ここまで来ると,後は「どうやって多体系の確率過程をどう解析的に解くか?」という数学上の技術的な問題に落とし込むことができます.
ここで多体系の確率過程の問題を,統計物理学で発達してきた計算手法を通じて解く理論を研究しています.具体的には,統計物理学における一つの計算技法として”kinetic theory”と呼ばれるものがあります.Kinetic theoryとは所謂「分子運動論」ですが,実は歴史的に完成した分子運動論の数理的な枠組みは「物理学の固有事情・分子という個別具体的な性質」を数学的な仮定としてあまり使っていません(※「分子がぶつかる」という物理的な描像というよりは,数学的に完成された抽象化された枠組みを”kinetic theory”とここでは呼んでいます).そこで,金澤はkinetic theoryの数学的技術を改良して,金融ABMの理論解析に応用する手法を開発しました(PRL 2018, PRE 2018).つまり,現象としてのアナロジーではなく,数理的なアナロジーを重視して,『統計物理学の数理を,金融のABMという別の問題に拡張する』という研究を行いました.
揺らぎの統計物理学
金澤は伝統的な意味での「揺らぎの統計物理学」の研究テーマ(非平衡定常系での「揺らぎの統計則」をミクロモデルから導出する)にも興味があります.以下,金澤が関わっている非平衡系の統計物理学の話についても触れます.
粉体系での非平衡ブラウン運動
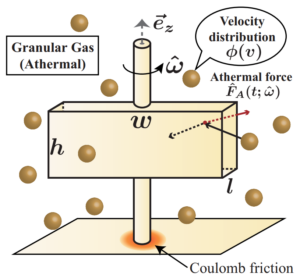
金澤は博士課程では加振粉体系(振動外力を加えてガス状に保った粉体系,非平衡定常系)における非平衡ブラウン運動を統計物理学の対象として研究し,非平衡定常系のミクロモデルからマクロな非平衡ブラウン運動のダイナミクスを解析的に扱う研究を行っていました(PRL 2015, Springer Theses).
また本論文の手法を(粉体系のような具体系を超えて)数理的に一般化すると,非平衡系状態の熱浴における揺らぎ(以下,「非熱的な揺らぎ」と呼ぶ)をモデル化する場合,幅広い条件下で非ガウス型のランジュバン方程式がマクロに表れうることが示せました.本研究は非ガウス型のランジュバン方程式を統計物理学的に導出する初めての体系的理論であり,確率過程の統計物理学基礎論として重要な仕事だと考えています.
アクティブマター系の非平衡ブラウン運動
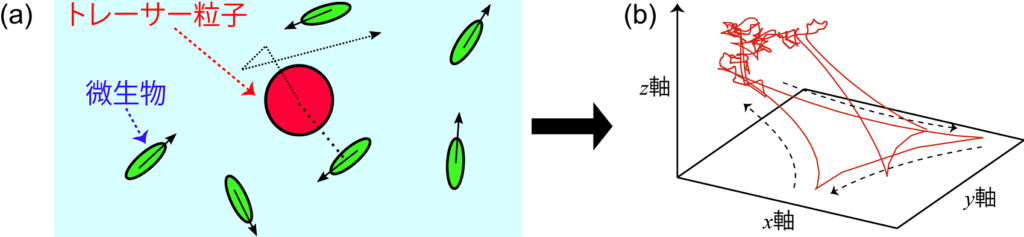
他にもアクティブマター系(生物物理系)における非平衡ブラウン運動の統計物理学の研究も行いました(Nature 2020).本研究では,遊走微生物のようなアクティブマター系を扱います.アクティブマター系は非平衡定常系であり,非平衡系統計物理学の対象となります.
Nature 2020では,このような系にトレーサー粒子(ブラウン粒子のような試験粒子)を入れたとき,『トレーサー粒子のダイナミクスがどのような確率モデルに従うか』という問いを統計物理学として研究しています.結果,レヴィ・フライトと呼ばれる異常拡散の確率モデルがマクロに現れることを,非平衡定常状態のミクロモデルから理論的に示しています.
これまでレヴィ・フライトは実験データに対する良いフィッティングモデルではありましたが,ミクロ的な基礎付けがない点が理論物理学としての問題点でした.一方,本研究は物理的に妥当な多体ミクロ系から,初めて統計物理的な手続きを得てレヴィ・フライトを導出する事例を提示したという意味で,レヴィ・フライトのミクロ的な基礎付けとして重要だと考えています.